ロボットを動かそう 
ステッピングモータは、電磁石にロータが引きつけられて回転しますので、電磁石の励磁切り替えパルスの速度で回転速度が決定されます。パルス速度と回転速度は比例関係になります。
モータ回転速度
（マウスポインタを移動すると速度が変わります）
ステッピングモータの回転角度は、モータ累積パルス数に比例しますので、モータが目標の回転角度になったらパルスを停止すれば、目標位置で止まることが可能です。
しかし、モータを始動時から早い速度で廻すことはできません。ロボットの重さを考慮して、パルス速度を加速する必要があります。ＤＣモータでは負荷に応じて自然に加速していきますが、ステッピングモータは入力パルスに追従した回転しかしませんので、モータが滑らかに廻るように加速→定常速度→減速するパルスを作り出す必要があります。ロボットの慣性を無視してステッピングモータを廻すと、トルク不足でモータが廻りませんし、モータが回転したとしても、動作がぎこちなくなります。
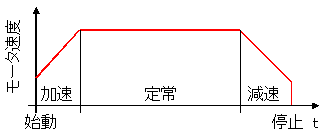
図１ モータの加減速運転
一方、ステッピングモータの回転が速くなると、モータのコイル励磁に回転が追いつかず、廻らなくなってしまうことがあります。この入力パルスにモータが追従できなくなる現象を脱調（だっちょう）といいます。定電流駆動方式では、トルク不足を防ぐため電流の立ち上がりが早くなるように高い電圧を印加しています。ある１パルスでモータコイルに流れる電流のグラフを図２に示します。モータ印加電圧が低い場合は電流の立ち上がり速度が遅く、モータコイルで十分な励磁ができません。そのためモータを廻そうとしても、トルク不足で廻りません。それに対し、定電流駆動方式では電流の立ち上がりが早く、高速時も十分なトルクを発生させることができます。
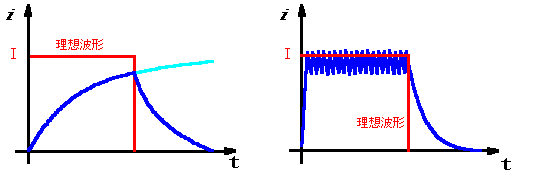
(a) 定電圧方式 (b) 定電流方式
図2 モータに流れる電流
ステッピングモータの加速パターンとして、等加速度近似曲線、Sin関数近似曲線、指数関数近似曲線などがあります。一般的には、等加速度近似曲線がよく利用されています。台形加速などと呼ばれている方式です。
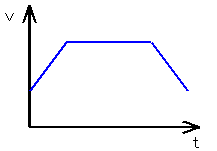
(a) 等加速近似曲線
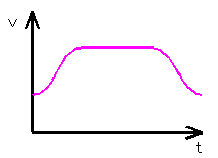
(b) Sin関数近似曲線
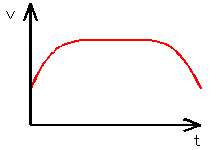
(c) 指数関数近似曲線
図３ モータの回転速度
等加速度加速において、パルスの加速度をα、スタート周波数をf0とするとt秒後のパルス周波数fは、
[pps] （1）
となり、t秒間にモータに与えたパルス数Nを用いて表現すると、
（2）
とtを消去することができます。したがって、加速度αはNパルス目のパルス周波数がfNのとき、
[pps/s] （3）
となります。 以上から、Nパルスの区間で加速中の第ｎパルス目の周波数fnは、
[pps] （4）
となり、その周期tnは、
[s] （5）
と求めることができます。
2001.10
戻る 